Journal of Radiology and Imaging
An International Peer-Reviewed Open Access Journal
ISSN 2399-8172


- Download PDF
- |
- Download Citation
- |
- Email a Colleague
- |
- Share:
-
- Tweet
-

Journal of Radiology and Imaging
Volume 6, Issue 1, December 2022, Pages 1–9
Original researchOpen Access
A revised Gaussian pencil beam model for calculation of the in-water dose caused by clinical electron-beam irradiation
-
Akira Iwasaki1,*
 , Shingo Terashima2,*
, Shingo Terashima2,* , Shigenobu Kimura3 , Kohji Sutoh3 , Kazuo Kamimura3 , Yoichiro Hosokawa2 , Masanori Miyazawa4 and Tatsuo Tabata5
, Shigenobu Kimura3 , Kohji Sutoh3 , Kazuo Kamimura3 , Yoichiro Hosokawa2 , Masanori Miyazawa4 and Tatsuo Tabata5
- 1 2-3-24 Shimizu, Hirosaki, Aomori 036-8254, Japan
- 2 Graduate School of Health Sciences, Hirosaki University, 66-1 Hon-cho, Hirosaki, Aomori 036-8564, Japan
- 3 Department of Radiology, Aomori City Hospital, 1-14-20 Katta, Aomori 030-0821, Japan
- 4 Technology of Radiotherapy Corporation, 2-1-2 Koishikawa, Bunkyo-ku, Tokyo 175-0092, Japan
- 5 Institute for Data Evaluation and Analysis, Sakai, Osaka 593-8311, Japan
*Corresponding authors: Akira Iwasaki, 2-3-24 Shimizu, Hirosaki, Aomori 036-8254, Japan. Tel: +172-33-2480; Email: fmcch384@ybb.ne.jp; Shingo Terashima, Graduate School of Health Sciences, Hirosaki University, 66-1 Hon-cho, Hirosaki, Aomori 036-8564, Japan. Tel: +81-172-39-5525; Email: s-tera@hirosaki-u.ac.jp.
Received 22 August 2022 Revised 31 October 2022 Accepted 12 November 2022 Published 23 November 2022
DOI: http://dx.doi.org/10.14312/2399-8172.2022-1
Copyright: © 2022 Iwasaki A, et al. Published by NobleResearch Publishers. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.
AbstractTop
Purposes: The dose in water caused by clinical electron-beam irradiation is mainly composed of the doses due to the direct electrons, the indirect electrons, and the contaminant X-rays. In this paper, an analytical method for 3-dimensional (3D) dose calculation in water for the direct electrons and for the direct-plus-indirect electrons is proposed in light of the electron Monte Carlo (eMC) datasets. Methods: The dose calculation was performed for square fields, based on a revised Gaussian pencil beam model, where the parallel beam depth-dose dataset under an infinitely large field was reconstructed from the depth-dose dataset of a fan beam with a finite field. We used a semi-infinite water phantom, setting the beam incident surface on the isocenter plane that is perpendicular to the beam axis. The dose calculation model sets an effective field at each dose calculation depth, where the effective field is larger than the geometrical field that the electron applicator forms on the basis of its divergent spread under the effective source-surface distance (SSDeff). Results and conclusions: By comparing the calculated datasets of depth dose (DD) and off-axis dose (OAD) in water with the eMC datasets for electron beams of E=6, 12, and 18 MeV by Wieslander and Knöös (2006), it has been found that the revised Gaussian pencil beam model is of practical use and has a bright prospect to give almost the same calculation results as the eMC datasets.
Keywords: electron-beam calculation; Gaussian pencil beam model; electron beams; electron applicator; linear accelerator
Research highlightsTop
The dose in water caused by the clinical electron-beam irradiation is mainly composed of the doses due to the direct electrons, the indirect electrons, and the contaminant X-rays. This paper introduces a revised Gaussian pencil beam model for 3-dimensional (3D) calculation of the direct electron dose or direct-plus-indirect dose in water in light of the electron Monte Carlo (eMC) datasets for square fields as reported by Wieslander and Knöös (2006). The revised Gaussian pencil beam model uses a parallel beam depth-dose dataset under an infinitely large field. This paper proposes a method for reconstructing the parallel beam depth-dose dataset under an infinitely large field using the depth-dose dataset of a fan beam with a finite field, and also proposes a generalized 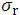 expression that is yielded based on the pencil beam parameter
expression that is yielded based on the pencil beam parameter 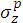 for off-axis to on-axis dose ratio calculations as produced by Bruinvis et al. (1983). By comparison with the eMC datasets, it may be concluded that the revised Gaussian pencil beam model can achieve accurate dose calculations in water.
for off-axis to on-axis dose ratio calculations as produced by Bruinvis et al. (1983). By comparison with the eMC datasets, it may be concluded that the revised Gaussian pencil beam model can achieve accurate dose calculations in water.
IntroductionTop
First of all, the present authors would like to emphasize the importance of this paper dealing with the Gaussian pencil beam model for electron beam dose calculations. This model is one of the older analytical dose calculation methods. However, the authors believe that the analytical methods are generally useful in understanding how electron beam radiation penetrates media and are generally fast to quantitatively calculate the transferred energy as dose. All the better if there is an analytical method that can accurately calculate the dose. The next section elaborates on the subject of this paper.
With respect to the electron beam therapy performed using high-energy electron beams from linear accelerators, Khan’s textbook [1] summarizes the following two characteristics, one as to the linear accelerators and the other as to the clinical points:
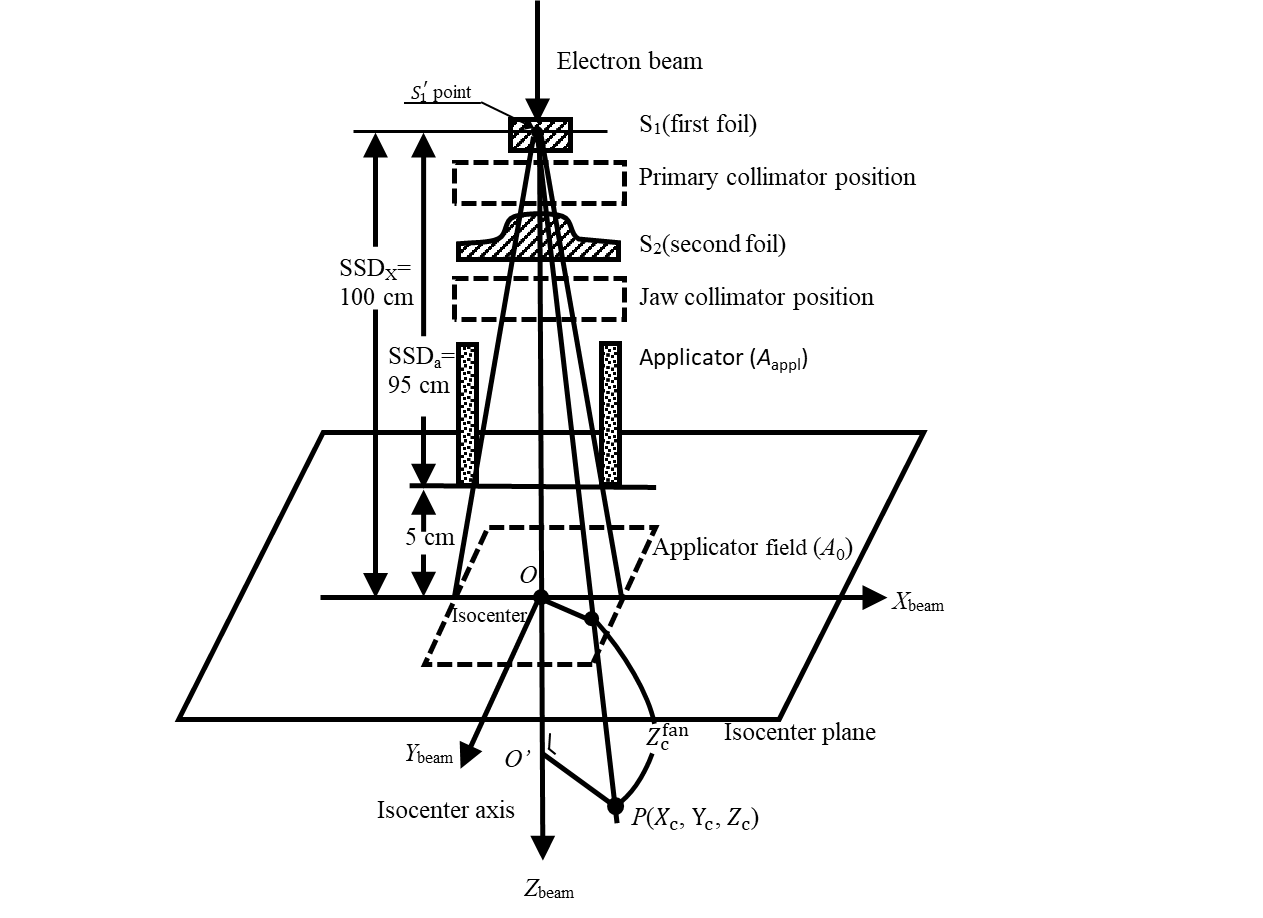
As to the linear accelerators: The field flatness and symmetry are obtained with a proper design of beam scatterers and beam defining collimators using one or more scattering foils (Figure 1), usually made up of lead, to widen the beam as well as to give a uniform dose distribution across the treatment field; and linear accelerators with scattering foil, having photon and multi-energy electron beam capabilities, have become increasingly available for clinical use. Recently, a dual-foil system has been used, which is composed of the first and second foils, and this foil system can generate broader electron beams with less X-ray contamination, especially at high energies.
As to the clinical points: It should be noted that the most useful energy for electrons is 6 to 20 MeV. At these energies, the electron beams can be used to treat superficial tumors (less than 5 cm deep) with a characteristically sharp drop-off in dose beyond the tumor. The principal applications are (a) the treatment of skin and lip cancers, (b) chest wall irradiation for breast cancer, (c) administering boost dose to nodes, and (d) the treatment of head and neck cancers. Although many of these sites can be treated with superficial X-rays, brachytherapy, or tangential X-ray beams, the electron-beam irradiation offers distinct advantages in terms of dose uniformity in the target volume and in minimizing the dose to deeper tissues.
The textbook also refers to the electron beam dose computation. The outline is as follows: (a) Major limitations of the empirical methods based on broad beams and slab geometries are their inability to predict effects on dose distribution of small fields, sudden changes in surface contour, small inhomogeneities, and oblique beam incidence. (b) An improvement over the empirical methods came about with the development of algorithms based on the age-diffusion equation first by Kawachi [2] in 1975. Although these algorithms are able to use semiempirically derived pencil beams that can be placed along the surface contour to predict effects of small fields and surface irregularity, their accuracy to calculate inhomogeneity correction is limited. (c) Major advancement in electron beam treatment planning occurred in the early 1980s. Methods were developed that were based on Gaussian pencil beam distributions calculated with the application of the Fermi-Eyges multiple scattering theory [3]. The methods are based on small-angle multiple scattering approximation. As a result, the elementary pencil beam penetrating a scattering medium is very nearly Gaussian in its lateral spread at all depths. Large-angle scattering events could cause deviations from a pure Gaussian distribution, but their overall effect on dose distributions is considered to be small.
On the other hand, electron Monte Carlo (eMC) methods [4-7] are today widely used in many electron-beam therapy applications because of the complexity of photon and electron transport (the eMC systems were first commercially built around 2000). Wieslander and Knöös [8, 9] have proposed implementation of a virtual linear accelerator (based on eMC simulations) into a commercial treatment planning system (TPS) to verify the TPS with respect to depth doses (DDs), off-axis doses (OADs or dose profiles), and output factors. They emphasize [9] that problems associated with conventional measurements can be avoided and properties that are considered unmeasurable can be studied. The eMC-based dose is separated into the dose from (a) direct electrons that have not interacted in the electron applicator, the dose from (b) indirect electrons that have interacted in the electron applicator, and the dose from (c) contaminant X-rays from the treatment head. They have summarized two groups of eMC-based dose datasets in water for electron beams of energies of 6, 12, and 18 MeV under a series of two electron applicators (shaping square-fields of 10×10 cm2 and 10×10/14×14 cm2). These groups of eMC-datasets are produced under a common virtual accelerator using two eMC simulations; one is installed in a given commercial TPS and the other is used as a standard simulation. The present paper refers to the datasets as “the W-K eMC dose datasets” or “the W-K eMC dose work”.
Iwasaki et al. [10] have developed an analytical method of calculating the 3-dimensional (3D) dose in water for the contaminant X-rays in light of the W-K eMC dose work. On the other hand, this present paper will propose another type of 3D dose calculation method, as a revised type of Gaussian pencil beam model, for both the direct electron beams and the direct-plus-indirect electron beams, similarly in light of the W-K eMC dose work. This dose calculation method utilizes a parallel beam depth-dose dataset in an infinitely broad field with the same incident electron-beam strength on the isocenter plane as the pencil beam composed of direct electrons or direct-plus-indirect electrons. We then propose a method for yielding the depth-dose dataset in an infinitely broad field from a depth-dose dataset yielded using a given electron applicator forming a finite field with the same incident electron-beam strength (Supplementary Figure 1). It should be emphasized that, for each electron beam, this method utilizes an effective beam field 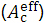 at each dose calculation depth level (Figure 2), letting the effective beam field be larger than the fan-beam field constructed simply using a given electron applicator. Finally, for the σ function used in the Gaussian pencil beam method, this paper uses a
at each dose calculation depth level (Figure 2), letting the effective beam field be larger than the fan-beam field constructed simply using a given electron applicator. Finally, for the σ function used in the Gaussian pencil beam method, this paper uses a 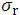 expression (as expressed later in equation 13) as functions of the pencil-beam axis depth and the electron beam energy, as regressed on the basis of the
expression (as expressed later in equation 13) as functions of the pencil-beam axis depth and the electron beam energy, as regressed on the basis of the 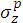 factor datasets proposed by Bruinvis et al. [11].
factor datasets proposed by Bruinvis et al. [11].
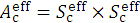 as shown in (b), where
as shown in (b), where 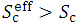 . “Phantom surface” in (b) is drawn on the basis of the phantom surface in (a) regarding the Zc plane.
. “Phantom surface” in (b) is drawn on the basis of the phantom surface in (a) regarding the Zc plane.
Materials and methodsTop
Symbols and units
This paper uses the following units: the length or depth is expressed in cm; the beam field is expressed in cm2; the electron-beam energy (E) is expressed in MeV; the dose is expressed in Gy; the extrapolated range  or
or  is expressed in cm; the Gaussian σ (
is expressed in cm; the Gaussian σ (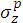 or
or 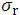 ) function is expressed in cm; and the angle in the sine formula is expressed in radian. It should also be noted that some other quantities are dimensionless (describing as “dimensionless”).
) function is expressed in cm; and the angle in the sine formula is expressed in radian. It should also be noted that some other quantities are dimensionless (describing as “dimensionless”).
Equational format
Strictly speaking, the experimental functions used in this paper usually have a lot of variables. For such functions, we take simplified formats as: If an expression of F(x,y) is established under a certain major premise of U0=1.0 and V0=2.0, we express this function as F(x,y), F (x, y: U0, V0), F(x,y: U0), F(x,y: V0), F(x,y: U0 = 1.0, V0 = 2.0) and so on case by case.
Dose calculation background
We use a clinical linear accelerator with dual-foil system as illustrated in Figure 1. On referring to Khan’s textbook [1] and Klevenhagen’s textbooks [12, 13], the present dose calculation method is described only for square beam fields (this is because the present dose calculation method is described in light of the W-K eMC dose work published only for square beam fields). On the other hand, it should also be emphasized that although the actual electron-beam irradiation is performed using an electron applicator forming a fan beam as shown in Figure 2a, the dose calculation is performed using its equivalent parallel beam irradiation as shown in Figure 2b. Let the surface perpendicular to the beam axis at the isocenter (O) be called the isocenter plane, and let the beam axis coincide with the Zbeam axis. We make an attempt to calculate the doses at arbitrary points in a semi-infinite water phantom whose surface coincides with the isocenter plane.
First, we enter general details of the dose calculation:
(a) The source-to-surface distance (SSD) used for electron beam irradiations is characterized [1] as: The virtual SSD (=SSDX in Figure 1) cannot give accurate inverse square law correction for dose at extended SSDs under all clinical conditions. This deviation from the inverse square law is caused by an additional decrease in dose because of a loss of side-scatter equilibrium in air and in phantom that is significant for small field sizes and low electron energies. An alternative method of correcting dose for the air gap between the electron applicator end and the isocenter plane (or the patient) is to determine the effective SSD (SSDeff), which gives the correct inverse square law relationship for the change in dose with distance. For the (SSDeff) evaluation for a given electron beam irradiation, this paper uses (SSDeff) datasets taken from a catalogue of Varian, as listed in Table 1.
| E(MeV) | Aappl=6×6 cm2 | Aappl=10×6 cm2 | Aappl=10×10 cm2 | Aappl=15×15 cm2 | Aappl=20×20 cm2 | Aappl=25×25 cm2 |
| 6 | 64.2 cm | 69.7 cm | 82.9 cm | 88.1 cm | 91.9 cm | 93.3 cm |
| 9 | 78.6 | 80.8 | 89.1 | 92.4 | 94.8 | 96.1 |
| 12 | 82.0 | 84.3 | 88.0 | 91.5 | 94.0 | 95.0 |
| 15 | 83.8 | 86.2 | 88.3 | 91.1 | 93.6 | 94.8 |
| 16 | 86.3 | 88.8 | 92.8 | 95.1 | 96.2 | 96.2 |
| 18 | 83.6 | 86.0 | 86.9 | 91.2 | 93.7 | 95.1 |
| 20 | 82.2 | 83.6 | 86.5 | 91.9 | 94.5 | 96.2 |
| 22 | 81.7 | 83.4 | 86.6 | 92.3 | 95.0 | 96.6 |
(b) For a given (SSDeff) fan beam irradiation as shown in Figure 2a, we take rectangular coordinate axes of Xbeam, Ybeam, and Zbeam by letting the Zbeam axis coincide with the beam axis and by letting the origins of the three axes be set at the isocenter (O). We set a dose calculation point of (Xc, Yc, Zc) on a Zc-depth plane with an origin mark (O') on the Zbeam axis. As described above, we take square beam fields, letting each beam field side (Sc) on the Zc-plane be parallel to the Xbeam or Ybeam axis. Aappl expresses the beam field measured at the electron applicator end; A0 expresses the beam field measured on the isocenter plane; and Ac expresses the beam field on the Zc plane, letting Ac=Sc × Sc.
(c) Figure 2b shows a parallel pencil-beam irradiation equivalent to the above fan beam irradiation, with respect to the dose at a point (Xc, Yc, Zc) on the Zc plane, taking the same Ac field at Zbeam = Zc with the same rectangular coordinate axes as illustrated in Figure 2a.
(d) This paper doses not perform the dose calculation directly using this Ac field, but performs it by setting a different field of 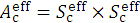 on the Zc plane as illustrated in Figure 2b. Let this
on the Zc plane as illustrated in Figure 2b. Let this 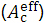 field be called the effective beam field. As described later in the discussion paragraph, the dose calculation is performed under
field be called the effective beam field. As described later in the discussion paragraph, the dose calculation is performed under 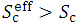 by taking into account of the side scatter of electrons beyond the Ac field.
by taking into account of the side scatter of electrons beyond the Ac field.
Next, we describe the dose calculation procedure using numerical expressions:
(e) Setting the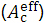 parallel beam field on the Zc plane, we perform the dose calculation based on the Gaussian pencil-beam algorithm. The dose at point (Xc, Yc, Zc) in Figure 2a is then set to be equal to the sum of the doses at point (Xc, Yc, Zc) in Figure 2b due to each small parallel pencil beam of
parallel beam field on the Zc plane, we perform the dose calculation based on the Gaussian pencil-beam algorithm. The dose at point (Xc, Yc, Zc) in Figure 2a is then set to be equal to the sum of the doses at point (Xc, Yc, Zc) in Figure 2b due to each small parallel pencil beam of 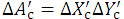 within the parallel beam field of
within the parallel beam field of 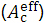 .
.
(f) We use the σ function as being evaluated by the beam energy (E) and also by the fan pencil-beam axis depth 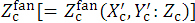 as illustrated in Figures 2, where point (
as illustrated in Figures 2, where point (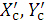 ) is set at the center point of each
) is set at the center point of each 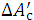 on the Zc plane. It should be noted that the present study evaluates the σ function without taking into account of the air layer above the phantom.
on the Zc plane. It should be noted that the present study evaluates the σ function without taking into account of the air layer above the phantom.
(g) The Gaussian pencil-beam algorithm also contains a special dose function of Dpara as described later in equation 4, expressing the parallel-beam depth-dose in an infinitely broad field, caused by the same incident beam intensity at the phantom surface position as shown in Figure 2a. This function is usually determined [1] from the measured depth-dose data of a broad field (e.g., 20 × 20 cm2). However, the clinical linear accelerators cannot generally set such large fields using electron applicators while keeping the same SSDeff index for a given electron-beam energy (Table 1). For this situation, we take the following procedures.
(h) First, by taking a fan beam depth-dose function Dfan with a finite A0 field, we reconstruct [1] a parallel beam depth-dose dataset of 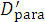 as
as
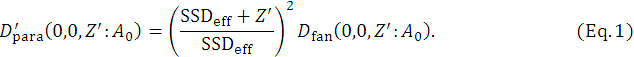
In Supplementary Figure 1, “DD line of Eq. 1” shows the  dataset of equation 1. Using the extrapolated range (Rp) of the
dataset of equation 1. Using the extrapolated range (Rp) of the 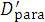 dataset, we obtain the depth
dataset, we obtain the depth  (E) of the point where the tangent to the descending linear portion of the eMC dotted line intersects the depth (Z or Z') line. Next, we reconstruct the corresponding parallel beam dose dataset of infinite field (A0 = ∞) as
(E) of the point where the tangent to the descending linear portion of the eMC dotted line intersects the depth (Z or Z') line. Next, we reconstruct the corresponding parallel beam dose dataset of infinite field (A0 = ∞) as
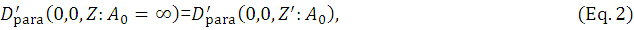
with 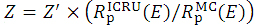 , where
, where  is another extrapolated range evaluated without a loss of side-scatter equilibrium in water, being recommended by the ICRU [14] as
is another extrapolated range evaluated without a loss of side-scatter equilibrium in water, being recommended by the ICRU [14] as

“DD line of Eq. 2” shows the dataset of the 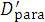 function in the left-hand side of equation 2, forming the extrapolated range that is equal to the
function in the left-hand side of equation 2, forming the extrapolated range that is equal to the  value. However, it has been found that this
value. However, it has been found that this 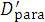 function cannot always express accurate doses at shallow depths of the phantom (“DD line of Eq. 4” is rebuilt under this adjustment, as described in the next item). It should also be noted [1, 8] that the field size of A0 performed by the given electron applicator should be relatively large. This is because, when the field size is relatively too small, the depth dose line shape is much different at the shallow depths from the shapes yielded using greater fields.
function cannot always express accurate doses at shallow depths of the phantom (“DD line of Eq. 4” is rebuilt under this adjustment, as described in the next item). It should also be noted [1, 8] that the field size of A0 performed by the given electron applicator should be relatively large. This is because, when the field size is relatively too small, the depth dose line shape is much different at the shallow depths from the shapes yielded using greater fields.
(i) It should be emphasized that each DD or OAD dataset of the W-K eMC dose work for a given electron beam energy (E) is normalized with a dose of 1.0 Gy per 100 MU at the maximum dose depth (dmax) caused by the mixed irradiation of direct electrons, indirect electrons, and contaminant photons under the use of an open electron applicator of Aappl = 20 × 20 cm2. Accordingly, the dose normalization for each beam is somewhat complicated. Here we introduce three factors of FACadjust, FAC1, and FAC2 to the 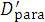 (0,0,Z:A0=∞) function of equation 2 by setting
(0,0,Z:A0=∞) function of equation 2 by setting 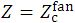 (Figure 2), describing as
(Figure 2), describing as
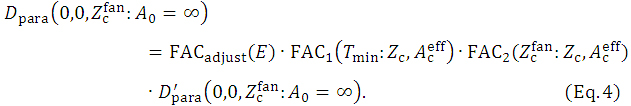
(j) For the three factors, we let have the following meanings as:
• FACadjust (E) is used as the adjusting factor for the factors of FAC1 and FAC2 by letting it be expressed simply as a function of the beam energy E (Supplementary Tables 1 and 2), showing FACadjust (E) 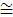 0.85. This factor is determined after evaluation of the FAC1 and FAC2 factors for a given irradiation condition.
0.85. This factor is determined after evaluation of the FAC1 and FAC2 factors for a given irradiation condition.
| W-K eMC DD & OAD datasets for the direct electron beams (KK=1-12) | E(MeV) | Aappl(cm2) | SSDeff cm) |  (cm) (cm) |
 (cm) (cm) |
FACadjust(E)(no unit) | Z1 (E)(cm) | Z2 (E)(cm) | Θ0 (E)(rad) | Wα (E)(no unit) |
| (i) Using the standard eMC (in stepped curves) | ||||||||||
| KK=1: fig. 3(b)-OAD (Zc=1 cm) under fig. 3(a)-DD | 6 | 10×10 | 82.9 | 2.834 | 3.291 | 0.884 | 1.5 | 2.5 | 1.776 | 0.104 |
| KK=2: fig. 3(c)-OAD (Zc =5 cm) under fig. 3(a)-DD | 6 | 10×10 | 82.9 | 2.834 | 3.291 | 0.884 | 1.5 | 2.5 | 1.776 | 0.104 |
| KK=3: fig. 5(b)-OAD (Zc =2 cm) under fig. 5(a)-DD | 12 | 10×10/14×14 | 91.5 | 5.915 | 6.002 | 0.914 | 1.0 | 4.3 | 1.56 | 0.0653 |
| KK=4: fig. 5(c)-OAD (Zc =10 cm) under fig. 5(a)-DD | 12 | 10×10/14×14 | 91.5 | 5.915 | 6.002 | 0.914 | 1.0 | 4.3 | 1.56 | 0.0653 |
| KK=5: fig. 3(e)-OAD (Zc =3 cm) under fig. 3(d)-DD | 18 | 10×10 | 86.9 | 8.996 | 8.453 | 0.806 | 0.95 | 8.0 | 1.68 | 0.150 |
| KK=6: fig. 3(f)-OAD (Zc =15 cm) under fig. 3(d)-DD | 18 | 10×10 | 86.9 | 8.996 | 8.453 | 0.806 | 0.95 | 8.0 | 1.68 | 0.150 |
| (ii) Using the commercial eMC (in dotted curves) | ||||||||||
| KK=7: fig. 3(b)-OAD (Zc =1 cm) under fig. 3(a)-DD | 6 | 10×10 | 82.9 | 2.834 | 3.291 | 0.908 | 1.5 | 2.5 | 1.754 | 0.0738 |
| KK=8: fig. 3(c)-OAD (Zc =5 cm) under fig. 3(a)-DD | 6 | 10×10 | 82.9 | 2.834 | 3.291 | 0.908 | 1.5 | 2.5 | 1.754 | 0.0738 |
| KK=9: fig. 5(b)-OAD (Zc =2 cm) under fig. 5(a)-DD | 12 | 10×10/14×14 | 91.5 | 5.915 | 6.101 | 0.910 | 1.0 | 4.5 | 1.560 | 0.0630 |
| KK=10: fig. 5(c)-OAD (Zc =10 cm under fig. 5(a)-DD | 12 | 10×10/14×14 | 91.5 | 5.915 | 6.101 | 0.910 | 1.0 | 4.5 | 1.560 | 0.0630 |
| KK=11: fig. 3(e)-OAD (Zc =3 cm) under fig. 3(d)-DD | 18 | 10×10 | 86.9 | 8.996 | 8.575 | 0.793 | 0.9 | 9.0 | 1.90 | 0.170 |
| KK=12: fig. 3(f)-OAD (Zc =15 cm) under fig. 3(d)-DD | 18 | 10×10 | 86.9 | 8.996 | 8.575 | 0.793 | 0.9 | 9.0 | 1.90 | 0.170 |
| W-K eMC DD & OAD datasets for the direct electron beams (KK=1-12) | 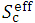 Zc, (E) (cm) Zc, (E) (cm) |
α1 (E) (cm) | b1 (E) (no unit) | c1 (E)(no unit) | T0 (Zc, E) (cm) | α2 (E) (cm) | b2 (E)(no unit) | c2 (E) (no unit) | 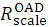 (Zc)(no unit) (Zc)(no unit) |
|
| (i) Using the standard eMC (in stepped curves) | ||||||||||
| KK=1: fig. 3(b)-OAD (Zc =1 cm) under fig. 3(a)-DD | 12.90 | 3.52E-08 | 19.72 | 9.80E-03 | 2.50 | 1.01E-37 | 86.10 | 6.60E-03 | 0.990 | |
| KK=2: fig. 3(c)-OAD (Zc =5 cm) under fig. 3(a)-DD | 17.65 | 3.52E-08 | 19.72 | 9.80E-03 | 6.27 | 1.01E-37 | 86.10 | 6.60E-03 | 0.619 | |
| KK=3: fig. 5(b)-OAD (Zc =2 cm) under fig. 5(a)-DD | 12.41 | 3.45E-19 | 44.77 | 8.45E-03 | 2.17 | 2.46E-36 | 82.08 | 1.20E-02 | 0.994 | |
| KK=4: fig. 5(c)-OAD (Zc =10 cm) under fig. 5(a)-DD | 22.99 | 3.45E-19 | 44.77 | 8.45E-03 | 10.90 | 2.46E-36 | 82.08 | 1.20E-02 | 39.063 | |
| KK=5: fig. 3(e)-OAD (Zc =3 cm) under fig. 3(d)-DD | 13.20 | 3.71E-23 | 53.73 | 8.50E-03 | 2.53 | 5.10E-37 | 83.30 | 1.30E-02 | 1.039 | |
| KK=6: fig. 3(f)-OAD (Zc =15 cm) under fig. 3(d)-DD | 27.86 | 3.71E-23 | 53.73 | 8.50E-03 | 15.10 | 5.10E-37 | 83.30 | 1.30E-02 | 36.115 | |
| (ii) Using the commercial eMC (in dotted curves) | ||||||||||
| KK=7: fig. 3(b)-OAD (Zc =1 cm) under fig. 3(a)-DD | 13.36 | 2.28E-07 | 17.89 | 9.83E-03 | 2.80 | 3.26E-38 | 87.35 | 6.28E-03 | 0.993 | |
| KK=8: fig. 3(c)-OAD (Zc =5 cm) under fig. 3(a)-DD | 17.77 | 2.28E-07 | 17.89 | 9.83E-03 | 6.80 | 3.26E-38 | 87.35 | 6.28E-03 | 1.548 | |
| KK=9: fig. 5(b)-OAD (Zc =2 cm) under fig. 5(a)-DD | 12.36 | 1.95E-15 | 36.15 | 9.46E-03 | 2.10 | 2.36E-35 | 79.86 | 1.10E-02 | 1.000 | |
| KK=10: fig. 5(c)-OAD (Zc =10 cm under fig. 5(a)-DD | 21.60 | 1.95E-15 | 36.15 | 9.46E-03 | 8.84 | 2.36E-35 | 79.86 | 1.10E-02 | 34.278 | |
| KK=11: fig. 3(e)-OAD (Zc =3 cm) under fig. 3(d)-DD | 13.20 | 1.70E-23 | 54.50 | 8.50E-03 | 2.47 | 1.60E-37 | 84.42 | 1.30E-02 | 1.028 | |
| KK=12: fig. 3(f)-OAD (Zc =15 cm) under fig. 3(d)-DD | 28.16 | 1.70E-23 | 54.50 | 8.50E-03 | 15.10 | 1.60E-37 | 84.42 | 1.30E-02 | 50.819 | |
• 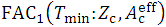 is used as the relative beam-strength factor, as shown later in Supplementary Figure 3, for point (
is used as the relative beam-strength factor, as shown later in Supplementary Figure 3, for point (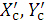 ) at the center of a small field of
) at the center of a small field of 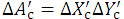 placed wholly inside the effective beam field of
placed wholly inside the effective beam field of 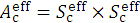 on a Zc plane (Figure 2 & Supplementary Figure 2). Note that we set FAC1 (Tmin:Zc,
on a Zc plane (Figure 2 & Supplementary Figure 2). Note that we set FAC1 (Tmin:Zc,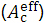 =0 for points (
=0 for points (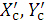 ) outside the
) outside the 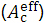 field, where Tmin is the minimum among the values of (T1, T2, T3, T4), expressing the distances to each of the four sides of
field, where Tmin is the minimum among the values of (T1, T2, T3, T4), expressing the distances to each of the four sides of 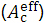 from point (
from point (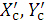 ) on the Zc plane as shown in Supplementary Figure 2. We let T0 (Zc:
) on the Zc plane as shown in Supplementary Figure 2. We let T0 (Zc: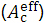 ) be a constant determined for the given square
) be a constant determined for the given square 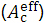 field on the Zc plane, then in Supplementary Figure 3, we set
field on the Zc plane, then in Supplementary Figure 3, we set
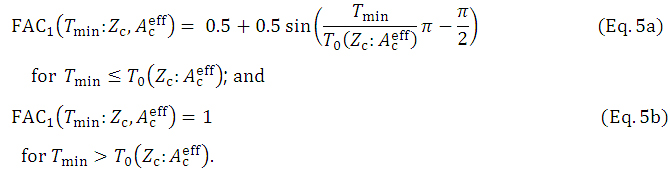
• 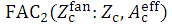 is introduced to estimate more accurate doses at relatively shallow depths of the phantom. This is because the
is introduced to estimate more accurate doses at relatively shallow depths of the phantom. This is because the 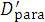 dose of equation 2 in this region is generally smaller than the reasonable dose (as may be understood from the dose differences between the DD lines of Eqs. 2 and 4 in Supplementary Figure 1). We divide the depth along the beam ray line (
dose of equation 2 in this region is generally smaller than the reasonable dose (as may be understood from the dose differences between the DD lines of Eqs. 2 and 4 in Supplementary Figure 1). We divide the depth along the beam ray line (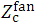 ) into three regions by setting two points at depths of Z1 and Z2 (Z1 < Z2) on the beam ray line as illustrated in Supplementary Figure 4. We then express the FAC2 factor as: For
) into three regions by setting two points at depths of Z1 and Z2 (Z1 < Z2) on the beam ray line as illustrated in Supplementary Figure 4. We then express the FAC2 factor as: For 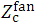 ≤ Z1, we set
≤ Z1, we set
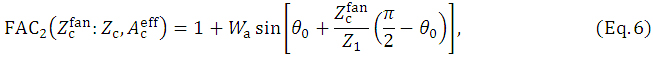
where θ0 is a constant (radian) given by the irradiation condition. It can be seen that the FAC2 factor ranges from 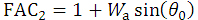 at
at 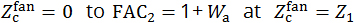 (where θ0>0 because the
(where θ0>0 because the 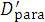 dose in the region of
dose in the region of 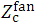 ≤Z1 is smaller than the reasonable dose). For Z1
≤Z1 is smaller than the reasonable dose). For Z1 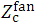 ≤ Z2, we set
≤ Z2, we set
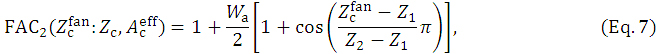
i.e., ranging from 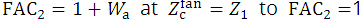 at
at 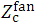 =Z2. For
=Z2. For 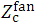 >Z2, we set
>Z2, we set

(k) The present work depends largely on the Dpara (0,0,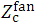 :A0=∞) function of equation 4 for accurately reproducing the W-K eMC datasets printed in the published paper. However, it has been found that it is very difficult to read off the printed data accurately in cases when they are at large depths especially beyond
:A0=∞) function of equation 4 for accurately reproducing the W-K eMC datasets printed in the published paper. However, it has been found that it is very difficult to read off the printed data accurately in cases when they are at large depths especially beyond  (Supplementary Figure 1). This is because these data are almost zero in the diagrams on a uniform scale. Particularly, serious badness happens for the OAD datasets on deep Zc (
(Supplementary Figure 1). This is because these data are almost zero in the diagrams on a uniform scale. Particularly, serious badness happens for the OAD datasets on deep Zc (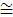
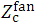 ) planes. In this case, by introducing a scale-reading factor of
) planes. In this case, by introducing a scale-reading factor of 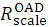 for each Zc plane, we re-evaluate the Dpara function as follows:
for each Zc plane, we re-evaluate the Dpara function as follows:
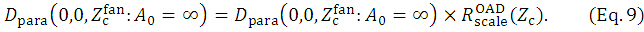
It has been found that, as listed in Table 2 and Supplementary Table 1, we take 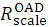 (Zc)
(Zc)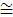 1 on shallow Zc planes (as described later, we should have taken
1 on shallow Zc planes (as described later, we should have taken 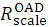 (Zc)=1; however, this paper takes values of
(Zc)=1; however, this paper takes values of 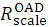 (Zc)<1 for simply making well-balanced OAD patterns with the corresponding eMC datasets). On deep Zc planes, we take
(Zc)<1 for simply making well-balanced OAD patterns with the corresponding eMC datasets). On deep Zc planes, we take 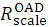 values much different from 1 (the general treatment is described in (r)).
values much different from 1 (the general treatment is described in (r)).
(l) The integration of the Gaussian distribution function within finite limits cannot be performed analytically. To evaluate this function necessitates the use of error function (erf). Thus convolution calculus shows that, for an electron beam of a rectangular cross section of 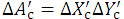 on the Zc plane (Supplementary Figure 2), the spatial dose for point (Xc, Yc, Zc) can be given [1] by
on the Zc plane (Supplementary Figure 2), the spatial dose for point (Xc, Yc, Zc) can be given [1] by
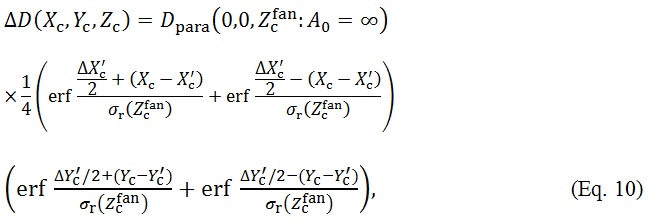
where 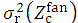 is the mean square radial displacement of electrons at depth
is the mean square radial displacement of electrons at depth 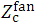 as a result of multiple Coulomb scattering.
as a result of multiple Coulomb scattering.
(m) The error function (erf) is defined thus:

This function is normalized so that erf (∞) = 1. It should be noted that, for a negative value of ε (this case happens when the dose calculation point is placed outside the 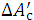 field), we can deal with equation 11 as
field), we can deal with equation 11 as

(n) Bruinvis et al. [7] have reported sets of 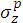 values for E=6,10,14 and 20 MeV, determined from electron beam OAD profiles measured at Z-depths using a 10×10 cm2 field. We found that the
values for E=6,10,14 and 20 MeV, determined from electron beam OAD profiles measured at Z-depths using a 10×10 cm2 field. We found that the 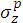 function can take the place of the
function can take the place of the 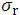 function in equation 10 (see the Appendix). Thus we reconstructed a
function in equation 10 (see the Appendix). Thus we reconstructed a 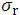 expression based on the sets of
expression based on the sets of 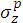 values, as follows:
values, as follows:
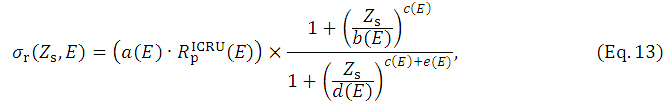
with

In this paper, we express the 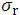 function also as
function also as 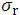 (Z) or
(Z) or 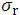 (
(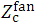 ) in a brief form only taking a phantom depth of Z or
) in a brief form only taking a phantom depth of Z or 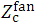 , respectively, for a given E-value. Supplementary Table 2 lists values (dimensionless) of a(E), b(E), c(E), d(E), and e(E) for each beam energy (E), [when a' (E) is used instead of a(E)∙
, respectively, for a given E-value. Supplementary Table 2 lists values (dimensionless) of a(E), b(E), c(E), d(E), and e(E) for each beam energy (E), [when a' (E) is used instead of a(E)∙ (E), the goodness-of-fit of equation 13 has been worse]. Supplementary Figure 5 compares two datasets of
(E), the goodness-of-fit of equation 13 has been worse]. Supplementary Figure 5 compares two datasets of 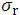 (Z,E) as a function of phantom depth Z for each beam energy (E): One is derived from equation 13 with the respective set of α(E) to e(E) values in Supplementary Table 2, and the other is the dataset of Bruinvis et al. [7]. Excellent agreement is seen between the two.
(Z,E) as a function of phantom depth Z for each beam energy (E): One is derived from equation 13 with the respective set of α(E) to e(E) values in Supplementary Table 2, and the other is the dataset of Bruinvis et al. [7]. Excellent agreement is seen between the two.
(o) To incorporate the dependence on beam energy (E) into equation 13, we analyzed each dataset of α(E) to e(E) in Supplementary Table 2 and obtained the following regression functions:
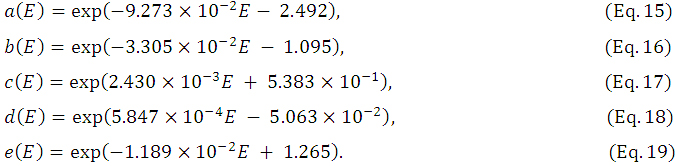
Supplementary Figure 6 compares two datasets of α(E)-e(E) on a semi-logarithmic scale: The straight lines show equations 15-19 in the energy range of E=0-25 MeV; and the dots, the values listed in Supplementary Table 2 for E=6, 10, 14, and 20 MeV. Supplementary Figure 7 compares two datasets of 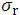 (Z) for E=6, 10, 14, and 20 MeV: The solid curves show equation 13 with equations 15-19; and the broken curves, the datasets reported by Bruinvis et al. [7] (Supplementary Figure 5). Looking at Supplementary Figures 5 and 7, we see that the agreement of each calculated dataset of
(Z) for E=6, 10, 14, and 20 MeV: The solid curves show equation 13 with equations 15-19; and the broken curves, the datasets reported by Bruinvis et al. [7] (Supplementary Figure 5). Looking at Supplementary Figures 5 and 7, we see that the agreement of each calculated dataset of 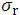 (Z) in the latter with the reported dataset is less satisfying. This is considered mainly due to the deviation of e(E) values given by equation 19 from the corresponding values in Supplementary Table 2 (Supplementary Figure 6). However, the noticeable differences from the datasets of Bruinvis et al. [7] due to this effect happen mainly at large Z-depths beyond the maximum of
(Z) in the latter with the reported dataset is less satisfying. This is considered mainly due to the deviation of e(E) values given by equation 19 from the corresponding values in Supplementary Table 2 (Supplementary Figure 6). However, the noticeable differences from the datasets of Bruinvis et al. [7] due to this effect happen mainly at large Z-depths beyond the maximum of 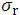 (Z) where the dose is relatively small. Accordingly, this effect is considered to cause no serious problems in ordinary circumstances. Supplementary Figure 8 shows the curves of
(Z) where the dose is relatively small. Accordingly, this effect is considered to cause no serious problems in ordinary circumstances. Supplementary Figure 8 shows the curves of 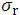 (Z) for E=2-30 MeV at intervals of 2 MeV generated by the generalized expression, i.e. equation 13 with equations 15-19.
(Z) for E=2-30 MeV at intervals of 2 MeV generated by the generalized expression, i.e. equation 13 with equations 15-19.
(p) The W-K eMC dose datasets are arranged for each of the electron-beam energies of E=6, 12, and 18 MeV using applicators of Aappl=10×10 cm2, Aappl=10×10/14×14 cm2 (10×10 is the opening field produced with a cerrobend insert in the original 14×14 shape), and Aappl=20×20 cm2. The dose datasets for each electron-beam energy (E) are separated into DD curves and OAD curves, where each dataset is normalized as described in (i). In the dose datasets acquired through the standard eMC simulation are composed of stepped curves of DD and OAD; and the dose datasets acquired through the commercial TPS are composed of dotted curves of DD and OAD. It should be noted that both the stepped and dotted datasets of OAD are classified in the X and Y directional OAD profiles; however, the present paper does not refer to the OAD differences caused by the X and Y directions. It should also be noted that the field size by each of the three applicators expresses the one measured at the applicator end position. As the present study uses the phantom whose surface coincides with the isocenter plane; therefor, these applicators are installed with an air gap of 5 cm above the phantom (Figure 1).
(q) We describe how to determine both values of 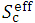 [Figure 2b & Supplementary Figure 2] and T0 (in equations 5a and 5b and Supplementary Figure 3) on an arbitrary Zc plane. Each DD and OAD data combination by W-K eMC dose work represents a DD dataset and a pair of OAD datasets at specific shallow and deep Zc depths, dividing into groups of stepped and dotted line datasets for each beam, as being divided into separate groups of the direct electron beams (Table 2) and the direct-plus-indirect electron beams (Supplementary Table 1). By analyzing the DD and OAD datasets through trial and error for each beam, we construct expressions to yield each pair of reasonable
[Figure 2b & Supplementary Figure 2] and T0 (in equations 5a and 5b and Supplementary Figure 3) on an arbitrary Zc plane. Each DD and OAD data combination by W-K eMC dose work represents a DD dataset and a pair of OAD datasets at specific shallow and deep Zc depths, dividing into groups of stepped and dotted line datasets for each beam, as being divided into separate groups of the direct electron beams (Table 2) and the direct-plus-indirect electron beams (Supplementary Table 1). By analyzing the DD and OAD datasets through trial and error for each beam, we construct expressions to yield each pair of reasonable 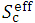 and T0 values over a wide range of Zc. For the
and T0 values over a wide range of Zc. For the 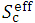 and T0 functions, this paper proposes the following expressions:
and T0 functions, this paper proposes the following expressions:

and

letting both sets of a1, b1, c1 values and of a2, b2, c2 values be constants simply determined by the beam energy (E) (Table 2 and Supplementary Table 1).
(r) Lastly, we describe how to generally perform the dose calculation at a point (Xc, Yc) on a Zc plane introducing a factor of Rscale (Xc, Yc, Zc) (this procedure happened because we cannot correctly read off the figures of the W-K eMC datasets of DD in case the dose points are at relatively large depths and/or large off-axis distances). Accordingly, using equation 4, we rewrite equation 10 as
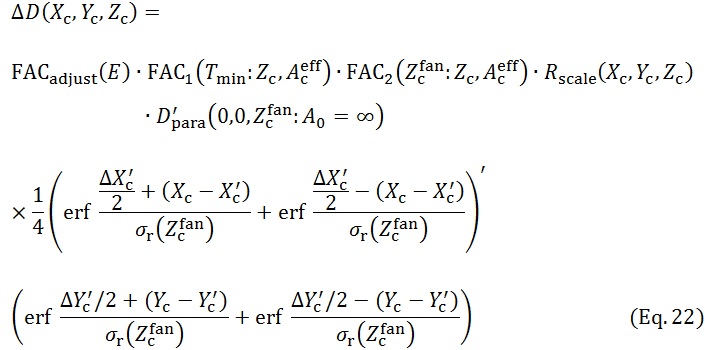
This paper simply uses Rscale (0,0, Zc) = 1 for the DD calculation. For the OAD calculation, we use values of Rscale (Xc, Yc, Zc)=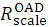 (Zc) as given in Table 2 and Supplementary Table 1 (each of the values was obtained by taking a well-balanced OAD pattern between the W-K eMC dataset and the calculated one).
(Zc) as given in Table 2 and Supplementary Table 1 (each of the values was obtained by taking a well-balanced OAD pattern between the W-K eMC dataset and the calculated one).
ResultsTop
The DD or OAD datasets reported in the W-K eMC dose work express the doses caused by (i) direct electrons and by (ii) direct-plus-indirect electrons. Moreover, each of the DD or OAD datasets is illustrated using stepped and dotted curves, where the stepped curves are yielded using the standard eMC simulation and the dotted curves are yielded using the commercial TPS. Here, we classify them into two for avoiding the confusion. One is listed in Table 2 taking the direct electron beams (KK=1-12), and the other is listed in Supplementary Table 1 taking the direct-plus-indirect electron beams (KK=13-24). It should be noted that the DD datasets were transcribed from Supplementary Figures 3(a), 5(a), and 3(d) in the W-K eMC dose work, and that the OAD datasets were similarly from Supplementary Figures 3(b), 3(c), 5(b), 5(c), 3(e), and 3(f).
Supplementary Figures 9 to 12 illustrate DD lines for (a) E=6 MeV, (b) E=12 MeV, and (c) E=18 MeV using the direct electron beams or the direct-plus-indirect electron beams through the standard eMC or the commercial eMC simulation approach.
• Supplementary Figure 9 illustrates sets of DD curves yielded using (i) the standard eMC for “the direct electron beams” of (a) E=6 MeV with Aappl=10×10 cm2 (KK=1 and 2), (b) E=12 MeV with Aappl=10×10/14×14 cm2 (KK=3 and 4), and (c) E=18 MeV with Aappl=10×10 cm2 (KK=5 and 6), where the KK numbers are listed in Table 2. Each set starts from the orange line showing the dataset of Dfan (0,0, Z':A0 ) letting Z=Z' (FanBeam-DD of FiniteField in Eq. 1), then reaches the gray line showing the dataset of 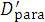 (0,0,Z':A0) letting Z=Z' (ParallelBeam-DD of FiniteField in Eq. 1), then reaches the yellow line showing the dataset of
(0,0,Z':A0) letting Z=Z' (ParallelBeam-DD of FiniteField in Eq. 1), then reaches the yellow line showing the dataset of 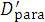 (0,0, Z:A0=∞) (ParallelBeam-DD of InfiniteField in Eq. 2), and lastly reaches the blue line showing the dataset of Dpara (0,0,
(0,0, Z:A0=∞) (ParallelBeam-DD of InfiniteField in Eq. 2), and lastly reaches the blue line showing the dataset of Dpara (0,0, 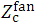 :A0=∞) letting Z=
:A0=∞) letting Z=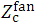 (ParallelBeam-DD of InfiniteField of Eq. 4). On each Z line in the diagrams of (a)-(c), the points of Z1 and Z2 are set (refer to equations 6 and 7); the point of
(ParallelBeam-DD of InfiniteField of Eq. 4). On each Z line in the diagrams of (a)-(c), the points of Z1 and Z2 are set (refer to equations 6 and 7); the point of  is set on the basis of the DD datasets on the orange and gray lines (refer to equation 2); and the point of
is set on the basis of the DD datasets on the orange and gray lines (refer to equation 2); and the point of  is set on the basis of the DD datasets on the blue and yellow lines (refer to equation 2). It should be noted that diagram (a) shows
is set on the basis of the DD datasets on the blue and yellow lines (refer to equation 2). It should be noted that diagram (a) shows  <
< , diagram (b) shows
, diagram (b) shows 
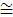
 , and diagram (c) shows
, and diagram (c) shows  <
< (we have no reasons why diagram (a) shows
(we have no reasons why diagram (a) shows  <
< ).
).
• Similarly, Supplementary Figure 10 illustrates sets of DD curves yielded using the commercial eMC for “the direct electron beams” of (a) E=6 MeV with Aappl=10×10 cm2 (KK=7 and 8), (b) E=12 MeV with Aappl=10×10/14×14 cm2 (KK=9 and 10), and (c) E=18 MeV with Aappl=10×10 cm2 (KK=11 and 12). It should also be noted that diagram (a) shows  <
< , diagram (b) shows
, diagram (b) shows 
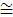
 , and diagram (c) shows
, and diagram (c) shows  <
< (we also have no reasons why diagram (a) shows
(we also have no reasons why diagram (a) shows  <
< ).
).
• Similarly, Supplementary Figure 11 illustrates sets of depth-dose (DD) curves yielded using the standard eMC for “the direct-plus-indirect electron beams” of (a) E=6 MeV with Aappl=10×10 cm2 (KK=13 and 14), (b) E=12 MeV with Aappl=10×10/14×14 cm2 (KK=15 and 16), and (c) E=18 MeV with Aappl=10×10 cm2 (KK=17 and 18). It should also be noted that diagram (a) shows  <
< , diagram (b) shows
, diagram (b) shows 
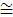
 , and diagram (c) shows
, and diagram (c) shows  <
< (we also have no reasons why diagram (a) shows
(we also have no reasons why diagram (a) shows  <
< ).
).
• Similarly, Supplementary Figure 12 illustrates sets of DD curves yielded using the commercial eMC for “the direct-plus-indirect electron beams” of (a) E=6 MeV with Aappl=10×10 cm2 (KK=19 and 20), (b) E=12 MeV with Aappl=10×10/14×14 cm2 (KK=21 and 22), and (c) E=18 MeV with Aappl=10×10 cm2 (KK=23 and 24). It should also be noted that diagram (a) shows  <
< , diagram (b) shows
, diagram (b) shows 
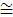
 , and diagram (c) shows
, and diagram (c) shows  <
< (we also have no reasons why diagram (a) illustrates
(we also have no reasons why diagram (a) illustrates  <
< ).
).
Under the  and
and  situations described above, the following features were obtained:
situations described above, the following features were obtained:
(a) Regarding the extrapolated range  (E), of the W-K eMC depth-dose dataset for each electron beam energy (E), both the standard eMC simulation and the commercial eMC TPS yield the almost the same extrapolated range even if the beam is composed of direct electrons or direct-plus-indirect electrons.
(E), of the W-K eMC depth-dose dataset for each electron beam energy (E), both the standard eMC simulation and the commercial eMC TPS yield the almost the same extrapolated range even if the beam is composed of direct electrons or direct-plus-indirect electrons.
(b) Both the standard eMC simulation and the commercial eMC TPS perform  (E)<
(E)< (E) only for the 18 MeV electron beams; however, both perform
(E) only for the 18 MeV electron beams; however, both perform  (E)>
(E)> (E) for the other energy beams.
(E) for the other energy beams.
(c) It should be noted that, even in the case of  (E)>
(E)> (E), we can build the expression of
(E), we can build the expression of 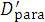 (0,0, Z: A0=∞) of equation 2 holding Z
(0,0, Z: A0=∞) of equation 2 holding Z
We finally describe the accuracy of the present dose calculation method, by comparing with the DD and OAD datasets reported in the W-K eMC dose work. Here, it should be noted for the factors listed from  (E) to
(E) to 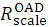 (Zc) in Table 2 and Supplementary Table 1 that each dataset of the factors of
(Zc) in Table 2 and Supplementary Table 1 that each dataset of the factors of  (E) to c2(E) have been derived from the corresponding DD dataset and the value for the
(E) to c2(E) have been derived from the corresponding DD dataset and the value for the 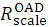 (Zc) factor is derived from the corresponding OAD dataset. This paper has introduced a factor of Rscale in equation 22. However, this factor is adopted only as
(Zc) factor is derived from the corresponding OAD dataset. This paper has introduced a factor of Rscale in equation 22. However, this factor is adopted only as 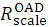 for each pair of OAD profiles on shallow and deep Zc planes. For the shallow Zc planes, the values of
for each pair of OAD profiles on shallow and deep Zc planes. For the shallow Zc planes, the values of 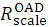
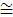 1 are used for making a well-balanced OAD pattern between the W-K eMC dataset and the calculated dataset. On the other hand, for the deep Zc planes, the values of
1 are used for making a well-balanced OAD pattern between the W-K eMC dataset and the calculated dataset. On the other hand, for the deep Zc planes, the values of 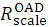 >>1 are used for making accurate Dpara (0,0,
>>1 are used for making accurate Dpara (0,0, 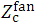 : A0=∞) values (equation 9). The reason is that we cannot help using such large
: A0=∞) values (equation 9). The reason is that we cannot help using such large 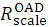 values because we use relatively much inaccurate data of Dpara (0,0,
values because we use relatively much inaccurate data of Dpara (0,0, 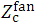 : A0=∞) or
: A0=∞) or 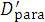 (0,0,
(0,0, 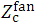 : A0=∞) at deep depths of
: A0=∞) at deep depths of 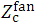 (equations 4, 10, and 22).
(equations 4, 10, and 22).
• Each of Supplementary Figures 13-18 illustrates a DD dataset and a pair of OAD datasets for the 6-, 12-, or 18-MeV direct electron beam using the standard or commercial eMC, indicating the corresponding KK-numbers in Table 2, where the sets of dots express the corresponding eMC dose results and the lines express the corresponding calculated dose results. It should be noted that diagram (a) is for DD, diagram (b) is for OAD on the shallow Zc plane, and diagram (c) is for OAD on the deep Zc plane. The eMC-OAD datasets on the deep Zc planes illustrate large amounts of electron side-scatter.
• Each of Supplementary Figures 19-24 similarly illustrates a DD dataset as diagram (a) and a pair of OAD datasets as diagrams (b) and (c) for the 6-, 12-, or 18-MeV direct-plus-indirect electron beam using the standard or commercial eMC, taking the corresponding KK-numbers in Supplementary Table 1. It can be understood that almost the same dose calculation tendency as in Supplementary Figures 13-18 is obtained.
DiscussionTop
Based on the concept of this revised Gaussian pencil beam model, we would like to discuss our future studies as follows:
(a) Khan’s textbook describes that the Gaussian pencil beam model calculates the dose only within the fan-beam field of Ac (Figure 2) formed by a given electron applicator, namely by letting the incident beam strength be zero outside the field. On the other hand, the present paper proposes to use the effective field of 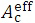 (Figure 2) that is greater than the Ac field. It should then be emphasized that the dose outside the Ac field can also be calculated with accuracy. In this case, the dose is produced by electrons mainly scattered from inside the fan-beam field (Ac). Accordingly, it may be emphasized that, even for such electrons, the parallel beam-axis DD function of infinite field (equation 2) can be used reasonably.
(Figure 2) that is greater than the Ac field. It should then be emphasized that the dose outside the Ac field can also be calculated with accuracy. In this case, the dose is produced by electrons mainly scattered from inside the fan-beam field (Ac). Accordingly, it may be emphasized that, even for such electrons, the parallel beam-axis DD function of infinite field (equation 2) can be used reasonably.
(b) In Figure 2a, if a phantom layer exists just above the isocenter plane or if an air gap layer exists just below the isocenter plane, these layers become kinds of heterogeneities for the standard irradiation. For the future study, we would take account of these heterogeneities also including heterogeneities within the phantom.
(c) This paper does not mention other types of beam fields and beam energies. These research themes are important for clinical use.
ConclusionTop
We have constructed a revised Gaussian pencil beam model on referring to the Khan’s textbook. We then utilized electron Monte Carlo (eMC) datasets of depth dose (DD) and off-axis dose (OAD) in water obtained using electron beams of E=6 MeV (Aappl=10×10 cm2), E=12 MeV (Aappl=10×10/14×14 cm2), and E=18 MeV (Aappl=10×10 cm2) as reported by Wieslander and Knöös (2006). The revised model has the following three features: (a) The parallel beam depth-dose dataset under an infinitely large field for each beam is reconstructed using the corresponding fan-beam depth-dose dataset. (b) The 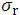 expression (equation 13 and Appendix A) is constructed based on the dataset produced by Bruinvis et al. (1983), as a function of depth (Z) and beam energy (E). (c) The
expression (equation 13 and Appendix A) is constructed based on the dataset produced by Bruinvis et al. (1983), as a function of depth (Z) and beam energy (E). (c) The 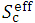 function (equation 20) is useful for estimating how the effective field varies with depth (Z).
function (equation 20) is useful for estimating how the effective field varies with depth (Z).
Conflicts of interest
This study was carried out in collaboration with Technology of Radiotherapy Corporation, Tokyo, Japan. This sponsor had no control over the interpretation, writing, or publication of this work.
ReferencesTop
[1]Khan FM, Gibbons JP. Khan’s The physics of radiation therapy; 5th edition. Philadelphia, USA; 2014. Website: www.lww.com
[2]Kawachi K. Calculation of electron dose distribution for radiotherapy treatment planning. Phys Med Biol. 1975; 20(4):571–577.Article Pubmed
[3]Eyges L. Multiple scattering with energy loss. Phys Rev. 1948; 74(10):1534–1535.Article
[4]Cygler JE, Daskalov GM, Chan GH, Ding GX. Evaluation of the first commercial Monte Carlo dose calculation engine for electron beam treatment planning. Med Phys. 2004; 31(1):142–153.Article Pubmed
[5]Ding GX, Duggan DM, Coffey CW, Shokrani P, Cygler JE. First macro Monte Carlo based commercial dose calculation module for electron beam treatment planning--new issues for clinical consideration. Phys Med Biol. 2006; 51(11):2781–2799.Article Pubmed
[6]Aubry JF, Bouchard H, Bessieres I, Lacroix F. Validation of an electron Monte Carlo dose calculation algorithm in the presence of heterogeneities using EGSnrc and radiochromic film measurements. J Appl Clin Med Phys. 2011; 12(4):2–14.Article Pubmed
[7]Lawrence SL, van Lieshout NHM, Charland PM. Assessment of Eclipse electron Monte Carlo output predication for various topologies. J Appl Clin Med Phys. 2015; 16(3):99–106.Article Pubmed
[8]Wieslander E, Knöös T. A virtual linear accelerator for verification of treatment planning systems. Phys. Med. Biol. 2000; 45(10):2887–2896.Article Pubmed
[9]Wieslander E, Knöös T. A virtual-accelerator-based verification of a Monte Carlo dose calculation algorithm for electron beam treatment planning in homogeneous phantoms. Phys Med Biol. 2006; 51(6):1533–1544.Article Pubmed
[10]Iwasaki A, Terashima S, Kimura S, Sutoh K, Kamimura K, et al. An analytical method for 3-dimensional calculation of the contaminant X-ray dose in water caused by clinical electron-beam irradiation. J Radiol Imaging. 2020; 4(2):7–16.Article
[11]Bruinvis IAD, Van Amstel A, Elevelt AJ, Van der Laarse R. Calculation of electron beam dose distributions for arbitrarily shaped fields. Phys Med Biol. 1983; 28(6):667–683.Article Pubmed
[12]Klevenhagen SC. Physics of electron beam therapy; Medical physics handbooks 13. Adam Hilger Ltd, Bristol and Boston.
[13]Klevenhagen SC. Current status of electron therapy-clinical and physical aspects. Megavoltage radiotherapy 1937-1987. British Journal of Radiology Supplement No. 22.
[14]International commission on radiation units & measurements. ICRU-Report 35; Radiation dosimetry: Electron beams and energies between 1 and 50 MeV. Bethesda, USA; 1984: Inc. (ICRU).


